Rumus Luas Permukaan Balok

Cara Mencari Luas Permukaan Balok . - Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi panjang dengan setidaknya salah satu pasang diantaranya berbeda. Bila ketiga pasang sisi bangun ruang tersebut berbentuk persegi (bujur sangkar) yang sama dan sebangun maka disebut sebagai kubus. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Untuk lebih jelas, lihat ilustrasi balok pada gambar di bawah ini.

Ilustrasi Balok

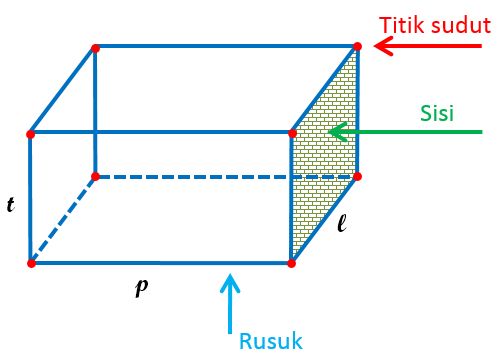
Pada gambar di atas p adalah panjang (rusuk) balok, l adalah lebar balok, dan t adalah tinggi balok. Bila pada artikel sebelumnya telah dibahas tentang rumus volume balok, maka pada artikel ini kita akan membahas secara detail atau rinci mengenai bagaimana cara menghitung luas permukaan/selimut balok termasuk mmenghitung luas alas balok berdasarkan luas selimut balok.

 

RUMUS LUAS BALOK

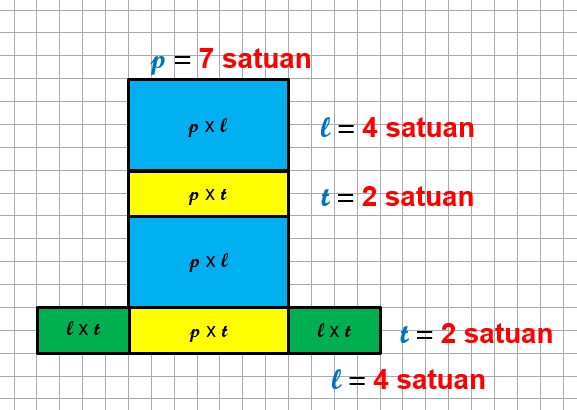
Dengan menganggap p adalah panjang dari balok, l adalah lebar balok, dan t adalah tinggi balok seperti yang dapat dilihat pada gambar di atas, maka untuk menghitung luas permukaan balok kita bayangkan dahulu membuka selimut balok menjadi jaring-jaring balok. Untuk lebih mudah membayangkan, misalkan kita mempunyai balok dengan panjang 7 satuan, lebar 4 satuan dan tinggi 2 satuan. Maka kita dapat menggambarkan jaring-jaring balok tersebut seperti gambar berikut :

Ilustrasi Jaring-Jaring Balok

Dari gambar tersebut kita lihat bahwa setiap sisi memiliki pasangan (ada 2 sisi yang sama, 2 sisi berwarna biru, 2 sisi berwarna kuning dan 2 sisi berwarna hijau ), sehingga kita bisa menghitung luas balok dengan cara :

 

Luas = 2 x ( p x l ) + 2 x ( p x t ) + 2 x ( l x t )

 

Dengan demikian cara mencari luas permukaan balok yang disimbolkan dengan L dapat dilakukan dengan menggunakan rumus :

 

 

Rumus mencari luas permukaan balok tersebut merupakan rumus dasar/awal yang bisa anda gunakan untuk banyak hal yang berkaitan dengan luas permukaan/selimut balok.

Untuk lebih mudah memahami bagaimana cara menghitung luas balok dengan rumus di atas akan digunakan beberapa contoh soal.

 

Contoh Soal 1: Menghitung Luas Balok

Hitung luas selimut/permukaan balok dibawah ini :

 

 

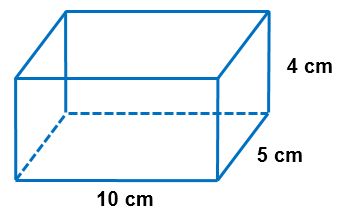
Jawab :

Diketahui :

p = 10 cm

l = 5 cm

t = 4 cm

L = 2 x ( p x l + p x t + l x t )

   = 2 x ( 10 x 5 + 10 x 4 + 5 x 4 )

   = 2 x ( 50 + 40 + 20 )

   = 2 x (110)

   = 220 cm²

Jadi luas permukaan balok tersebut 220 cm² .

 

Contoh Soal 2: Menghitung Luas Balok

Sebuah balok memiliki panjang 8 cm, lebar 5 cm, dan tinggi 2 cm. Hitung Luas permukaan balok tersebut.

Jawab :

Diketahui :

p = 8 cm

l = 5 cm

t = 2 cm

L = 2 x ( p x l + p x t + l x t )

   = 2 x ( 8 x 5 + 8 x 2 + 5 x 2 )

   = 2 x ( 40 + 16 + 10 )

   = 2 x (66)

   = 132 cm²

Jadi luas permukaan balok tersebut 132 cm² .

RUMUS LUAS SISI BALOK

Ada tiga buah sisi balok yang berbeda. Untuk lebih jelasnya akan diterangkan dengan menggunakan gambar. Misalkan kita memiliki balok dengan panjang p , lebar l , dan tinggi t satuan seperti gambar di bawah ini.

 

 

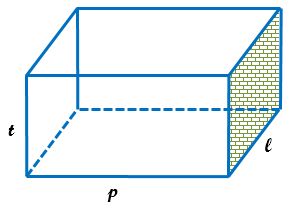
Maka kita bisa menghitung Luas sisi balok dengan rumus seperti yang ada pada gambar di bawah ini.

 

 

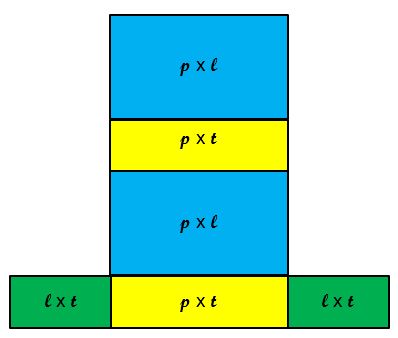
RUMUS LUAS ALAS BALOK adalah L_alas = p x l

RUMUS LUAS SISI SAMPING BALOK adalah L_{sisi samping} = p x t

RUMUS LUAS SISI DEPAN/BELAKANG BALOK adalah L_{sisi depan} = l x t

 

Contoh Soal 3: Menghitung Luas Salah Satu Sisi Balok

Hitung luas sisi yang diarsir pada gambar balok di bawah ini jika luas seluruh permukaan balok adalah 108 cm² .

 

 

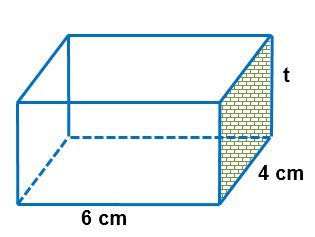
Jawab :

Diketahui :

p = 6 cm

l = 4 cm

L = 108 cm²

Yang akan kita hitung luasnya adalah luas sisi depan/belakang yang dinyatakan dengan l x t .

 

L = 2 x ( p x l + p x t + l x t )

108 = 2 x ( 6 x 4 + 6 x t + 4 x t )

108 = 2 x ( 24 + 6t + 4t )

108 = 2 x (24 + 10t)

108 = 2 x (24 + 10t)

108 / 2 = 24 + 10t

54 = 24 + 10t

24 + 10t = 54

10t = 54 - 24

10t = 30

t = 30 / 10

t = 3 cm.

Luas daerah yang diarsir adalah :

L_arsir = l x t = 4 x 3 = 12 cm² .

Jadi luas sisi balok yang diarsir tersebut adalah 12 cm² .

 

RUMUS LUAS ALAS BALOK

Untuk mendapatkan luas alas balok kita bisa menggunakan rumus dasar untuk menghitung luas permukaan balok. Yang harus dipahami, luas yang kita hitung adalah luas bidang datar yang merupakan perkalian dari panjang dan lebar sebagaimana seperti yang tampak pada daerah yang diarsir pada contoh gambar berikut ini.

 

 

Contoh Soal 4: Menghitung Luas Alas Balok

Hitung luas alas balok jika panjang balok 20 cm, tinggi 5 cm dan luas permukaan balok adalah 700 cm² .

Jawab :

Diketahui :

p = 20 cm

t = 5 cm

L = 700 cm²

Yang akan kita hitung luasnya adalah luas alas balok yang dinyatakan dengan p x l .

 

L = 2 x ( p x l + p x t + l x t )

700 = 2 x ( 20 x l + 20 x 5 + l x 5 )

700 = 2 x ( 20 l + 100 + 5 t )

700 = 2 x (100 + 25 l )

700/2 = 100 + 25 l

350 = 100 + 25 l

350 – 100 = 25 l

250 = 25 l

25 l = 250

l = 250 / 25 = 10 cm.

Sehingga Luas Alas Balok adalah : L_{alas balok} = p x l = 20 x 10 = 200 cm² .

 

LUAS PERMUKAAN DAN PERBANDINGAN RUSUK

Dalam kehidupan sehari-hari kita sering menggunakan perbandingan. Misalnya, jumlah buku Shinta tiga kali lebih banyak daripada jumlah buku Dani. Untuk balok pun kita bisa menggunakan perbandingan, misalnya panjang balok 10 kali dari lebar balok, dan lebar balok 2 kali dari tinggi balok, dan sebagainya. Berikut ini contoh penggunaan rumus luas permukaan balok dengan menggunakan perbandingan panjang rusuknya.

Contoh Soal 5: Luas permukaan Balok dan Perbandingan Rusuk

Sebuah balok memiliki perbandingan panjang 5 kali dari tingginya dengan lebar 3 kali dari tingginya. Jika luas permukaan balok adalah 184 cm², hitung ukuran sesungguhnya balok tersebut.

Jawab :

Diketahui :

p = 5 x t = 5t

l = 3 x t = 3t

L = 184 cm²

 

L = 2 x ( p x l + p x t + l x t )

184 = 2 x ( 5t x 3t + 5t x t + 3t x t )

184 = 2 x ( 15t² + 5t² + 3t² )

184 = 2 x (23t²)

184 / 2= (23t²)

92 = (23t²)

23t² = 92

t² = 92 / 23

t² = 4

t = √4 = 2 cm.

 

Sehingga :

Panjang balok : p = 5 x t = 5 x 2 = 10 cm

Lebar balok : l = 3 x t = 3 x 2 = 6 cm

Dengan demikian balok tersebut memili panjang 10 cm, lebar 6 cm dan tinggi balok adalah 2 cm.

 

 

RUMUS LUAS BALOK DAN RUMUS VOLUME BALOK

Luas permukaan dan volume balok sering kali berhubungan. Tidak jarang dalam soal ataupun permasalahan akan kita temui. Saya sudah pernah membahas secara rinci Cara menghitung volume balok, yang pada intinya (sekaligus mengingatkan kembali) bahwa Rumus Volume Balok adalah :

 

 

 

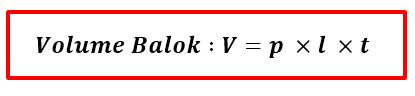
Agar tidak terlalu panjang lebar, berikut ini beberapa contoh soal yang berkaitan dengan penggunaan rumus luas dan volume balok.

 

Contoh Soal 6: Menghitung Luas Permukaan Balok

Sebuah balok memiliki panjang 10 cm, lebar 5 cm. Hitung Luas permukaan balok tersebut jika diketahui Volume Balok adalah 150 cm³ .

Jawab :

Diketahui :

p = 10 cm

l = 5 cm

V = 150 cm³

Pertama-tama kita cari tinggi balok terlebih dahulu dengan menggunakan rumus volume balok

V = p x l x t

150 = 10 x 5 x t

150 = 50 x t

50 x t = 150

t = 150 / 50 = 3 cm

Selanjutnya kita bisa menghitung luas permukaan balok :

L = 2 x ( p x l + p x t + l x t )

   = 2 x ( 10 x 5 + 10 x 3 + 5 x 3 )

   = 2 x ( 50 + 30 + 15 )

   = 2 x (95)

   = 190 cm²

Jadi luas permukaan balok tersebut 190 cm² .

 

Contoh Soal 7: Menghitung Volume Balok

Sebuah balok memiliki lebar 4 cm dan tinggi 2 cm dengan Luas permukaan balok 136 cm² . Hitung volume Balok tersebut.

Jawab :

Diketahui :

l = 4 cm

t = 2 cm

L = 136 cm²

Pertama-tama kita cari panjang balok terlebih dahulu dengan menggunakan rumus luas permukaan balok

L = 2 x ( p x l + p x t + l x t )

136 = 2 x ( p x 4 + p x 2 + 4 x 2 )

136 = 2 x (4p + 2p + 8 )

136 = 2 x (6p + 8 )

136/2 = (6p + 8 )

68 = 6p + 8

68 – 8 = 6p

60 = 6p

6p = 60

p = 60/6 = 10 cm

 

Selanjutnya kita hitung volume Balok :

V = p x l x t = 10 x 4 x 2 = 80 cm³ .

Jadi volume balok tersebut adalah 80 cm³ .

 

Contoh Soal 8: Menghitung Volume Balok

Sebuah balok memiliki ukuran dengan perbandingan panjang, lebar, dan tinggi berturut-turut adalah 8, 5 dan 3. Jika volume balok tersebut adalah 960 cm³ , berapakah luas permukaan balok?

Jawab :

Diketahui :

perbandingan rusuk :

p : l : t = 8 : 5 : 3

 

Pertama-tama kita cari ukuran panjang, lebar dan tinggi balok yang sebenarnya.

Misalkan ukuran sebenarnya adalah nilai perbandingan dikali dengan sebuah konstanta z, sehingga :

p = 8 x z = 8z

l = 5 x z = 5z

t = 3 x z = 3z

 

V = p x l x t

960 = 8z x 5z x 3z

960 = 120z³

120z³ = 960

120z³ = 960

z³ = 960 / 120

z³ = 8

z = 2 (kenapa??? Karena 2³ = 2 x 2 x 2 = 8)

Sehingga :

p = 8 x z = 8 x 2 = 16 cm.

l = 5 x z = 5 x 2 = 10 cm.

t = 3 x z = 3 x 2 = 6 cm.

 

Selanjutnya kita menghitung luas permukaan balok :

L = 2 x ( p x l + p x t + l x t )

    = 2 x ( 16 x 10 + 16 x 6 + 10 x 6 )

    = 2 x ( 160 + 96 + 60 )

    = 2 x ( 316)

    = 632 cm² .

Jadi luas permukaan balok tersebut adalah 632 cm² .

 

Tips Rumus Luas Permukaan Balok

• Seperti biasa, untuk lebih memahami penggunaan rumus luas permukaan balok dan volume balok anda harus sering berlatih terutama untuk menjawab soal


• Untuk menambah wawasan, baca juga artikel saya terdahulu mengenai Rumus Volume Balok dan Perbandingan senilai dan berbalik nilai