Rumus Phytagoras

Cara menghitung sisi segitiga dengan rumus phytagoras Rumus phytagoras sudah sangat terkenal. Hingga kini rumus tersebut menjadi primadona atau bahan yang wajib diajarkan mulai di sekolah dasar. Phytagoras yang lahir sekitar 570 sebelum masehi. Rumus Phytagoras merupakan hasil pemikiran phtagoras saat sedang mempelajari geometri di mesir. Phytagoras sangat tertarik dengan segitiga yang memiliki ratio 3:4:5. Phytagoras merupakan intelektual pertama yang menemukan bahwa kuadrat dari hipotenus atau sisi miring (yang lebih panjang) dari segitiga siku-siku memiliki nilai yang sama dengan penjumlahan kuadrat kedua sisi lainnya. Kalau bahasa jaman sekarang:

ce kuadrat sama dengan a kuadrat tambah be kuadrat ;).

 

Ilustrasi segitiga siku-siku dengan rumus phytagoras

Untuk membahas lebih mendalam mengenai rumus phytagoras dapat dilihat pada beberapa contoh berikut ini.

 

Contoh Sederhana Penggunaan Rumus Phytagoras

Sebuah segitiga siku-siku memiliki sisi yang saling tegak lurus dengan panjang 3 centimeter dan 4 centimeter. Berapakah panjang hipotenus atau sisi miring dari segitiga siku-siku tersebut ?

Jawab:

Diketahui :

a = 3 cm, b = 4 cm

Hitung : c = ....?

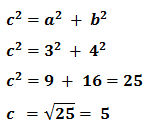
Jadi panjang hipotenus atau sisi miring segitiga siku-siku tersebut adalah 5 cm.

 

Contoh Menghitung Panjang Sisi Segitiga

Sebuah segitiga siku-siku memiliki sisi miring dengan panjang 15 cm sedangkan salah satu sisi lainnya adalah 9 cm. Berapakah panjang sisi yang satunya lagi ?

Jawab:

Diketahui :

c = 15 cm, a = 9 cm

Hitung : b = ….?

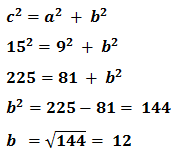
Jadi panjang sisi segitiga yang satunya lagi adalah 12 cm.

Perhatikan, bahwa panjang sisi segitiga siku-siku tersebut mengikuti pola 3:4:5. Sama seperti pada contoh sebelumnya.

Bila anda menemukan pola yang sama maka dapat menggunakan pola tersebut untuk menentukan panjang sisi-sisi segitiga siku-siku. Untuk lebih jelasnya lhat beberapa contoh berikut.

 

Menghitung Cepat Sisi Miring Segitiga Siku-siku

Hitunglah sisi miring dari segitiga siku-siku yang memiliki sisi tegak lurus :

a) 6 meter dan 8 meter

a) 18 satuan dan 24 satuan

a) 33 cm dan 44 cm

Jawab:

 

a) Memperhatikan pola bilangan pyhtagoras 3:4:5, jika 6 = 2x 3 dan 8 = 2x 4 maka sisi miring nya adalah 2 x 5 = 10 meter.

 

b) Karena 18 = 6 x 3 dan 24 = 6 x 4 maka sisi miring segita memiliki ukuran :
6x 5 = 30 satuan.

 

c) Karena 33 = 11 x 3 dan 44 = 11 x 4 maka sisi miring segita memiliki ukuran :
11x 5 = 55 cm.

 

Cara Menghitung Cepat Sisi Segitiga Siku-siku

Contoh soal: Jika sisi miring dari segitiga siku-siku adalah 40 cm dan salah satu sisi tegak lurusnya adalah 32 cm, maka hitunglah panjang sisi segitiga yang satunya lagi.

Jawab:

c = 40 cm, b = 32 cm.

Karena sisi miring: c = 40 = 8 x 5 dan sisi tegak b = 32 = 8 x 4 maka sisi segitiga yang satunya lagi memiliki ukuran :
8x 3 = 24 cm.

Daftar Pola Bilangan Tripel Phytagoras

Bilangan tripel phytagoras dengan perbandingan 3:4:5 seperti yang telah digunakan pada beberapa contoh diatas merupakan salah satu pola yang dapat digunakan sebagai pendekatan untuk menghitung secara cepat panjang sisi segitiga siku-siku. Masih banyak bilangan bulat dengan pola seperti bilangan phytagoras tersebut yang juga dapat anda gunakan, seperti contoh pola bilangan dibawah ini untuk panjang sisi yang kurang dari 100:

 

Daftar Bilangan Tripel Phytagoras

a	b	c
3	4	5
5	12	13
7	24	25
8	15	17
9	40	41
11	60	61
12	35	37
13	84	85
16	63	65
20	21	29
28	45	53
33	56	65
36	77	85
39	80	89
48	55	73
65	72	97

 

Tips Menghitung dengan Rumus Phytagoras

• Pola bilangan phytagoras memang sangat banyak. Anda tidak perlu menghapal semua itu, akan tetapi cukup menghapal beberapa buah saja yang menurut anda mudah dihapal. Sisanya gunakan saja rumus phytagoras : c² = a² + b²


• Untuk lebih memahami dan mengingat rumus phytagoras, sebaiknya sering-sering berlatih berhitung secara manual.